⇒ ` 3x 2y 12` ⇒ `3x = 12 2y` ⇒ `x (12 2y )/3` putting y = 6 , we get `x = (12 2 (6 ))/3` = 0 Putting y = 3 , we get ` x = (12 2 (3))/3` = 2 Putting y = 0 we get `x = (12 0 )/3 ` = 4 Thus, we get the following table giving the two points on the line represented by the equation ` x / 2 y/ 3 = 2` Graph for theMath Input NEW Use textbook math notation to enter your math Try itSimilarly, solutions in the triangle with vertices (1,1), (3/2,0) and (2,0) can never leave Exercises Graph the nullclines and discuss the possible fates of solutions for the following sys

Answers
(x^2+y^2-1)^3=x^2y^3 graph
(x^2+y^2-1)^3=x^2y^3 graph-Hint First, and for the sake of simplicity, write 3x− y = −2 as and ax 2y = 3 More Items 2y=3x Subtract x from both sides \frac {2y} {2}=\frac {3x} {2} Divide both sides by 2 y=\frac {3x} {2} Dividing by 2 undoes the multiplication by 2 x=32y1 x = y^2 2 2 x = 2y^2 2y 3 3 x^2 = 1/8y This question is from textbook Answer by Edwin McCravy () ( Show Source ) You can put this solution on YOUR website!



How Do You Graph The Line X Y 2 Socratic
Transcript Question 26 (OR 1st question) Find the area bounded by the curves y = √𝑥, 2y 3 = x and x axis Given equation of curves y = √𝑥 2y 3 = x Here, y = √𝑥 y2 = x So, it is a parabola, with only positive values of y Drawing figure Drawing line 2y 3 = x on the graph Finding point of intersection of line and curve y = √A m= 2, passes through (3,0) c m= 2, xintercept = 3 b m=2, yintercept = 3 d m= 1/2, passes through (0, 3) 93 Find the slope of the line passing through the points (1, 4) and (7,2) a 3 c 1/3 b 1 d 0 94 An isometry preserves congruence b False a True 95 Find theUnlock StepbyStep (x^2y^21)^3=x^2y^3 Extended Keyboard Examples
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music Explanation x2 y2 − 6x 2y − 6 = 0 → x2 − 6x y2 2y = 6 → x2 − 6x 9 y2 2y 1 = 691 → (x −3)2 (y 1)2 = 42 which is the standard form for a circle with center (3, −1) and radius 4 graph {x^26xy^22y6=0 81, 968, 5404, 348} Answer linkGraph y=x^23 y = x2 − 3 y = x 2 3 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 3 x 2 3 Tap for more steps Use the form a x 2 b x c a x 2 b x
Answer to Consider the hyperbola with equation x^2y^2=1 a) Graph the hyperbola there are two points on this curve where x =3 Find their (x,y) Refer Explanation section Given y=x^32x^2x dy/dx=3x^24x1 (d^2y)/(dx^2)=6x4 dx/dy=0=>3x^24x1 x=(b)sqrt(b^2(4*a*c))/(2a) x=(4)sqrt(4^2(4*3*1))/(2*3Question 7757 1 How do you plot x = 2y, y = x 2, y = 2x and y = x ק 2 on a graph Which one of the above formulas describes a line Found 2 solutions by josmiceli, MathLover1



Show Graphically The System Of Linear Equations Br X 2y



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora
0 y 2 Solution We look for the critical points in the interiorSteps Using the Quadratic Formula y= \frac { { x }^ { 2 } 3x2 } { { x }^ { 2 } 1 } y = x 2 − 1 x 2 − 3 x 2 Variable x cannot be equal to any of the values 1,1 since division by zero is not defined Multiply both sides of the equation by \left (x1\right)\left (x1\right) Variable x cannot be equal to any of the values − 1, 1X 2 y 2 − 1 = x 2 / 3 y , which can easily be solved for y y = 1 2 ( x 2 / 3 ± x 4 / 3 4 ( 1 − x 2)) Now plot this, taking both branches of the square root into account You might have to numerically solve the equation x 4 / 3 4 ( 1 − x 2) = 0 in order to get the exact x interval Share answered Dec 22 '12 at 1731 Christian



Draw Graphs Of The Equation 3x 2y 4 And X Y 3 0 In The Same Graph And Find The Coordinat Youtube




Solve Graphically The System Of Equations X Y 3 3x 2y 4 Mathematics Topperlearning Com Ja91bwemm
(i) The graph of Z f(x,y)= X^2 2y^2 2; The two solutions are (7,5) and (5,1) To solve the system of equations {(x2y=3,qquad(1)),(x^2y^2=24,qquad(2))} We must realize that there may be two solutions, since equation (2) is a hyperbola, and hyperbola may cross a linear equation at two points First, solve for x in equation (1) x2y=3 x=32y Plug this into equation (2) x^2y^2=24 (32y)^2y^2=24 912y4y^2y^2=24 912y3y^2Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Substitute the x x value 2 2 into f ( x) = 1 √ 4 − x f ( x) = 1 4 x In this case, the point is ( 2, ) ( 2, )



How To Solve The System Of Equations 2x Y 1 And 3x 2y 5 By Graphing Socratic




Answers
Simple and best practice solution for x2y3=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean " =0 " It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculationsTo graph two objects, simply place a semicolon between the two commands, eg, y=2x^21;
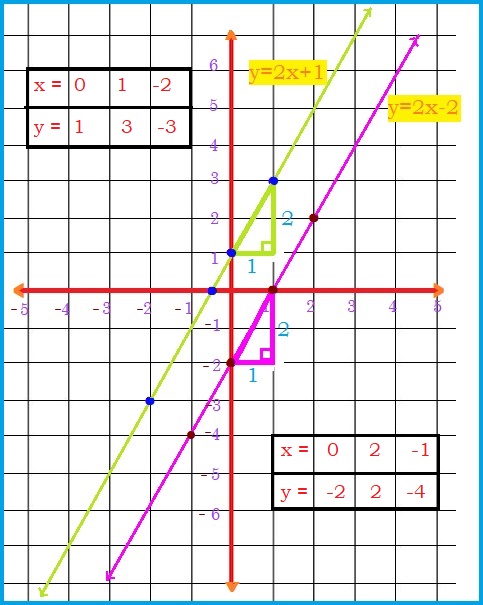



How Do You Solve The System By Graphing Y 2x 1 And Y 2x 2 Socratic
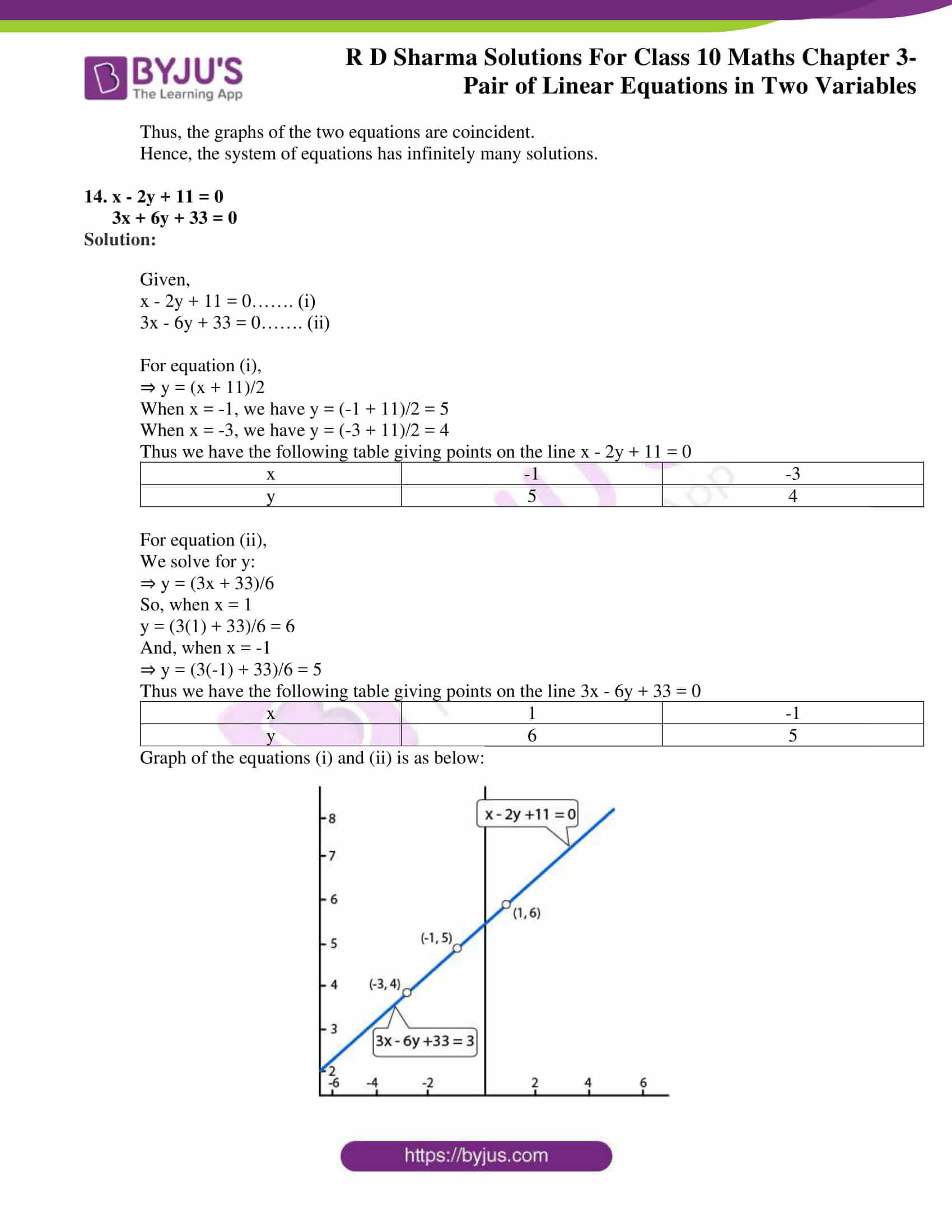



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
Subtracting x 2 from itself leaves 0 \left (y\sqrt 3 {x}\right)^ {2}=1x^ {2} ( y 3 x ) 2 = 1 − x 2 Take the square root of both sides of the equation Take the square root of both sides of the equation y\sqrt 3 {x}=\sqrt {1x^ {2}} y\sqrt 3 {x}=\sqrt {1x^ {2}} y 3 x = 1 − x 2 y 3 x = − 1 − x 2Divide 2, the coefficient of the x term, by 2 to get 1 Then add the square of 1 to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}2x1=\frac {y1} {3}1 Square 1 x^ {2}2x1=\frac {y2} {3} Add \frac {y1} {3} to 1 \left (x1\right)^ {2}=\frac {y2} {3}Y = x 2 1 implicitly Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test) We are using the idea that portions of y y are functions that satisfy the given equation, but that y y is not actually a function of x x



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora



1
You can put this solution on YOUR website!Explore math with our beautiful, free online graphing calculator Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more Log InorSign Up − 6 2 2 − x − 2 2 1 − 6 − 2 2 − x − 2 2 2 − 6 2 2 − x − 6 2 3 − 6 − 2 2 − x − 6 2 4 − 6 2 2 − x 2 2Graph x=1/2y^2 Combine and Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola
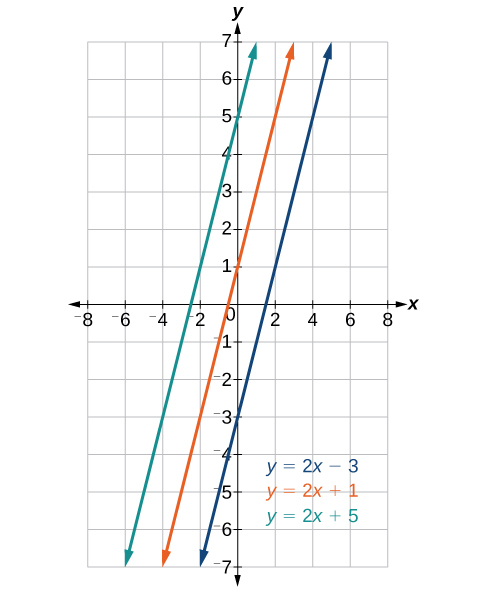



Determining Whether Graphs Of Lines Are Parallel Or Perpendicular College Algebra
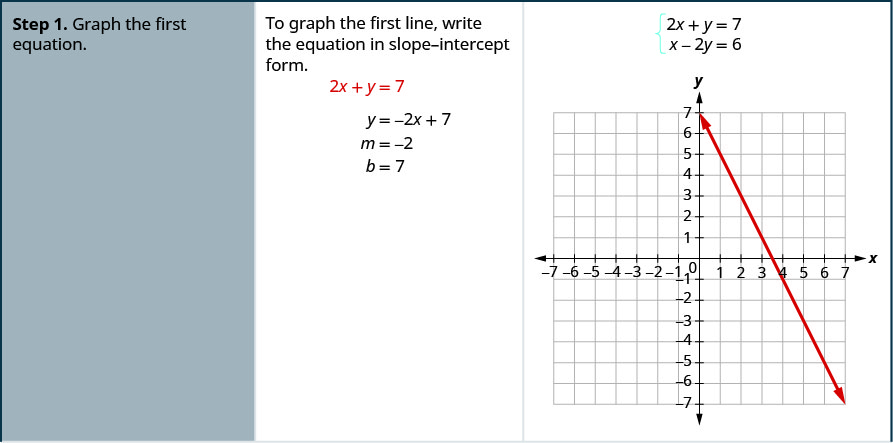



Solve Systems Of Equations By Graphing Elementary Algebra
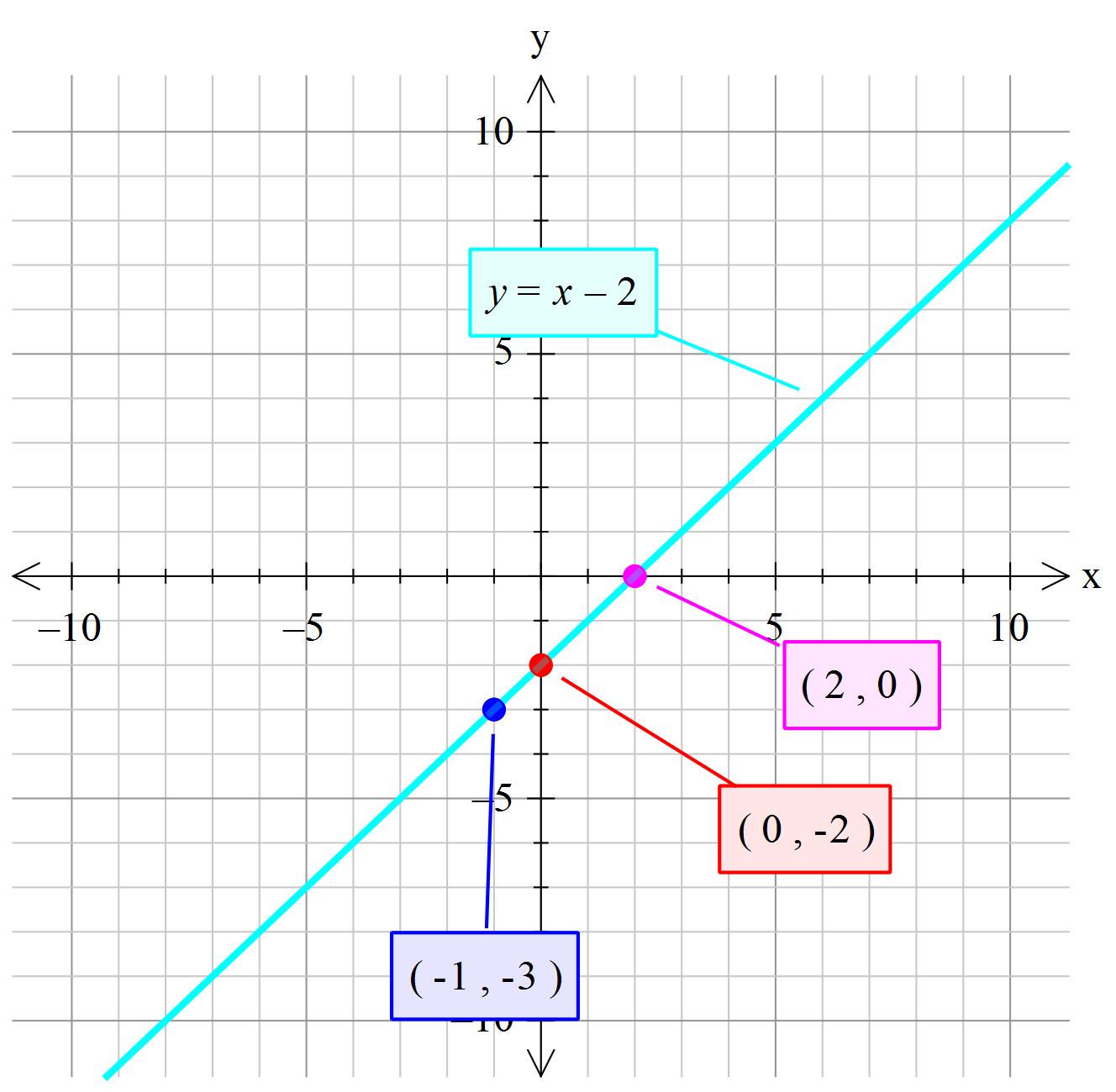
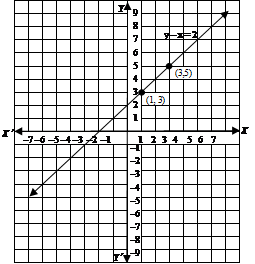
Section 43 Double Integrals over General Regions In the previous section we looked at double integrals over rectangular regions The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral, ∬ D f (x,y) dA ∬ D f ( x, y) d A where D D is any regionPlot x^2y^2x Natural Language;SolutionShow Solution We have x – 2y = 3 ⇒ y=\frac { x3 } { 2 } When x = 1, y = = –1 When x = –1, y = = –2 Plotting points (1, –1) & (–1, –2) on graph paper & joining them, we get straight line as shown in fig This line is required graph of equation x – 2y = 3




Graph Using Intercepts



2
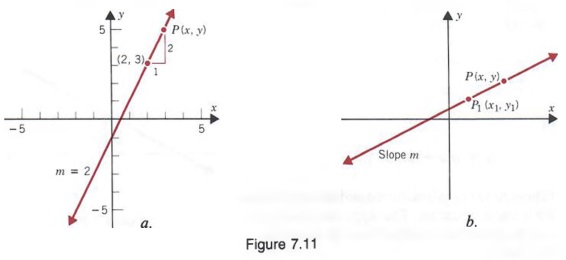
Rewrite the equation as − 3 2 x 2 = 0 3 2 x 2 = 0 − 3 2 x 2 = 0 3 2 x 2 = 0 Add 3 2 3 2 to both sides of the equation x 2 = 3 2 x 2 = 3 2 Since the expression on each side of the equation has the same denominator, the numerators must be equal x = 3 x = 3 Multiply both sides of the equation by 2 21 x 3y z = 10 3x 2y – 2z = 3 2x – y – 4z = 7 1) choose two equations and eliminate one variable 3x 2y – 2z = 3 2 2x – y – 4z = 7 3x 2y – 2z = 3 4x – 2y – 8z = 14 7x – 10z = 11 2) choose two different equations and eliminate the same variable {y} x 3y z = 10 3 2x – y – 4z = 7 x 3y z = 10Example 7 In the graph of y = 3x 2 the slope is 3 The change in x is 1 and the change in y is 3 y = mx b is called the slopeintercept form of the equation of a straight line If an equation is in this form, m is the slope of the line and (0,b) is the point at which the graph intercepts (crosses) the y



Graph Of Linear Equation Ax By C 0 In Two Variables Where A And B Not Equal To Zero Mathematics Knowledgeuniverseonline Com



Graphs And Solutions To Systems Of Linear Equations Beginning Algebra
The only thing we need is to identify the slope and yintercept and apply it to the graph Answer and Explanation 1 We are given the function {eq}y=\dfrac{3}{2}x3 {/eq} Transcript Ex63, 5 Solve the following system of inequalities graphically 2x y > 1, x 2y < 1 First we solve 2x y > 1 Lets first draw graph of 2x y = 1 Drawing graph Checking for (0,0) Putting x = 0, y = 0 2x y > 1 2(0) (0) > 1 0 > 1 which is false Hence origin does not lie in plane 2x y 6 So, we shade right side of line Now we solve x 2y < 1 Lets first draw graph of x 2y = 1Original equation 3x 2y 6 = 0 Subtract 2y from both sides to get 3x 6 = 2y Divide each side by (2) (3x 6)/(2) = (2y)/(2) → (3x)/(2) (6)/(2




If 2x 3 Y 2 1 6 0 And X 2 2y 3 3 Then




So My Applied Maths Lecturer Emailed Me To Graph This On Valentines Day X 2 Y 2 1 3 X 2y 3 0 9gag
2 days ago Which of the following applies to the graph of x 2y = 6?CH33 The Derivative as a Function Ex62數學系卡安很閒 所以決定拯救沒辦法用slader和chegg的莘莘學子Find all points (x, y) on the graph of g(x) = (1/3)* x^3 (3/2) x^2 1(ii) The graph of 3 = X^2 2y^2 2 1 Both (i) and (ii) are counter maps 2 Both (i) and (ii) are contour maps 3 (i) is a level curve, and (ii) is a counter map 4 (ii) is a level curve



Graph Graph Equations With Step By Step Math Problem Solver




A Function Is Defined By F X Y X 3 Y Xy Chegg Com
NCERT Solutions for Class 10 Maths Chapter 3 Exercise 32 Question 7 Summary For the graphs of the equations x y 1 = 0 and 3x 2y 12 = 0, the coordinates of the vertices of the triangle formed by these lines and the xaxis are (1, 0), (4, 0), and (2, 3)Graph y=2 (x1)^23 y = −2(x − 1)2 3 y = 2 ( x 1) 2 3 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 2 a = 2 h = 1 h = 1 k = 3 k = 3Graph each horizontal parabola and give the domain and range Place them in the form (y k) = 4p (x h) where the vertex is (h, k), the focus is (hp, k) the end of the focal chord (or latus rectum) are the points (hp,k2p), (hp, k2p) the directrix is the vertical line whose equation is x



11 3 Graphing Linear Equations Part 1 Mathematics Libretexts



Draw The Graphs Of Each Of The Equation X 2y 3 0 And 4x 3y 1 0 On The Same Graph Mathematics Topperlearning Com V7f7f21
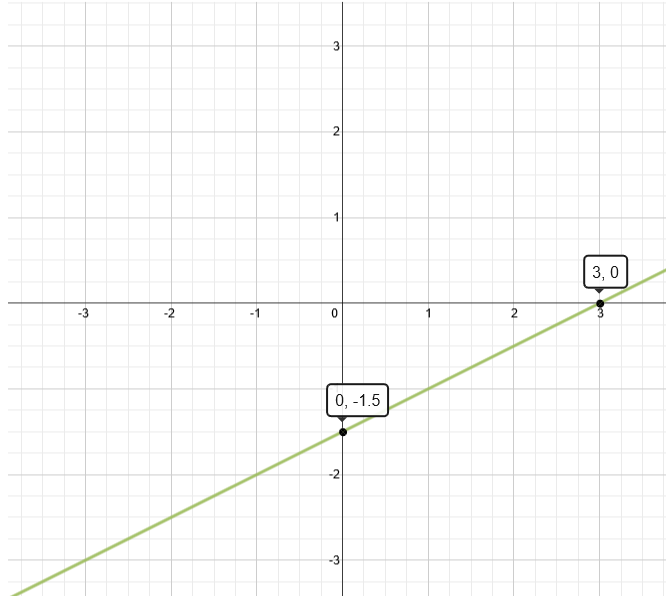
Maximize xyz in x^22y^23z^2Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music2x2y=3 Geometric figure Straight Line Slope = 1 xintercept = 3/2 = yintercept = 3/2 = Rearrange Rearrange the equation by subtracting what is to the right of the Find the equation of the line which is parallel to the line \displaystyle{3}{x}{4}{y}={1} and passes through the midpoint of the line segment joining \displaystyle{\left({1},{2}\right)} and




How Do You Graph The Line X Y 2 Socratic




Sketch The Region Bounded By The Graphs Of The Equations X Y 2 2y X 1 Y 0 Study Com
Demonstration of how to graph an equation in slope intercept form interpreting the slope at the coefficient of x and the constant term as the yinterceptSloStep 1 Just a quick note When you have an equation just plot two points x=0 and find y using the equation and x=0 and find x using the equation Then draw a line between two point Graph y = 1/2x 3/2 There are two ways of doing this One If a line has intercepts a on x axis and b on y axis, then its equation is x a y b = 1 Now we can write 3x 2y = 1 as x 1 3 y 1 2 = 1 Hence, intercept on x axis is 1 3 and on y axis is 1 2 Two We can find x intercept by putting y = 0 and y intercept by putting x = 0 (this method is



Graph Graph Equations With Step By Step Math Problem Solver




Draw The Graph Of 3x 2y 1 And 2x Y 4 And Write The Co Ordinates Of The Point Where The Graphs Brainly In
Click here👆to get an answer to your question ️ Draw a graph of the line x 2y = 3 From the graph, find the coordinates of the point when i) x = 5 ii) y = 0 Example \(\PageIndex{1}\) Determine whether \((1, −2)\) and \((−4, 1)\) are solutions to \(6x−3y=12\) Solution Substitute the \(x\) and \(y\)values intoY3=1/2(x2) multiply equation by 2 2(y3)=x2 2y6=x2 2y=x26 2y=x4 /2 y=(1/2)x2 y= 1/ 2 x 2 Assume values of x and plug in the equation to get values of y



Solution The Lines With Equations X 2y 3 And 3y Ax 2 Are Perpendicular To Each Other Find The Value Of A A 6 B 3 2 C 3 2 D 6 E 22
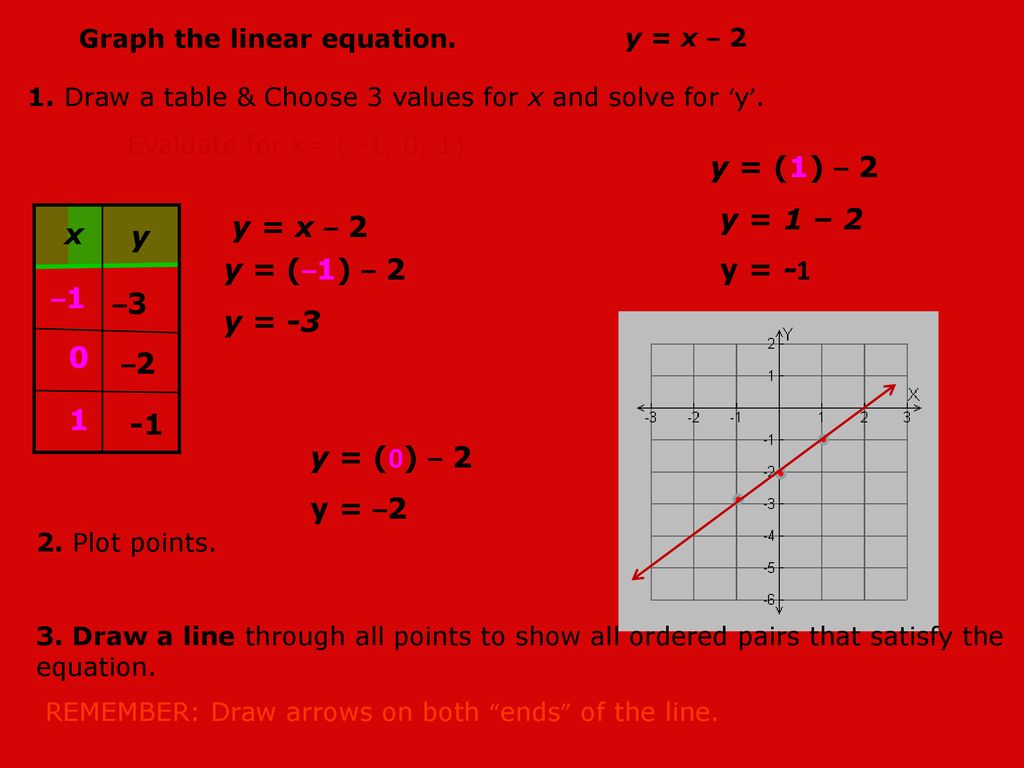



Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download
First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More ExamplesY=3x1 Polynomials Algebra Calculator can simplify polynomials, but it only supports polynomials containing the variable x Here are some examples x^2 x 2 (2x^2 2x), (x3)^2 The equation of a line in slopeintercept form is ∙ y = mx b where m represents the slope and × ×b, the yintercept y = 1 3x − 2 is in this form ⇒ slope = 1 3 and yintercept = − 2 plot the point (0, − 2) using the slope, from 2 go up 1, across 3 to the right and mark the point, that is (3,1)




1 Graph The System Of Linear Equations Solve The System And Interpret Your Answer 3y 2 Homeworklib




Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange
X^3 x^2 y x y^2 y^3 Natural Language;Problem 2 Determine the global max and min of the function f(x;y) = x2 2x2y2 2y2xy over the compact region 1 x 1;




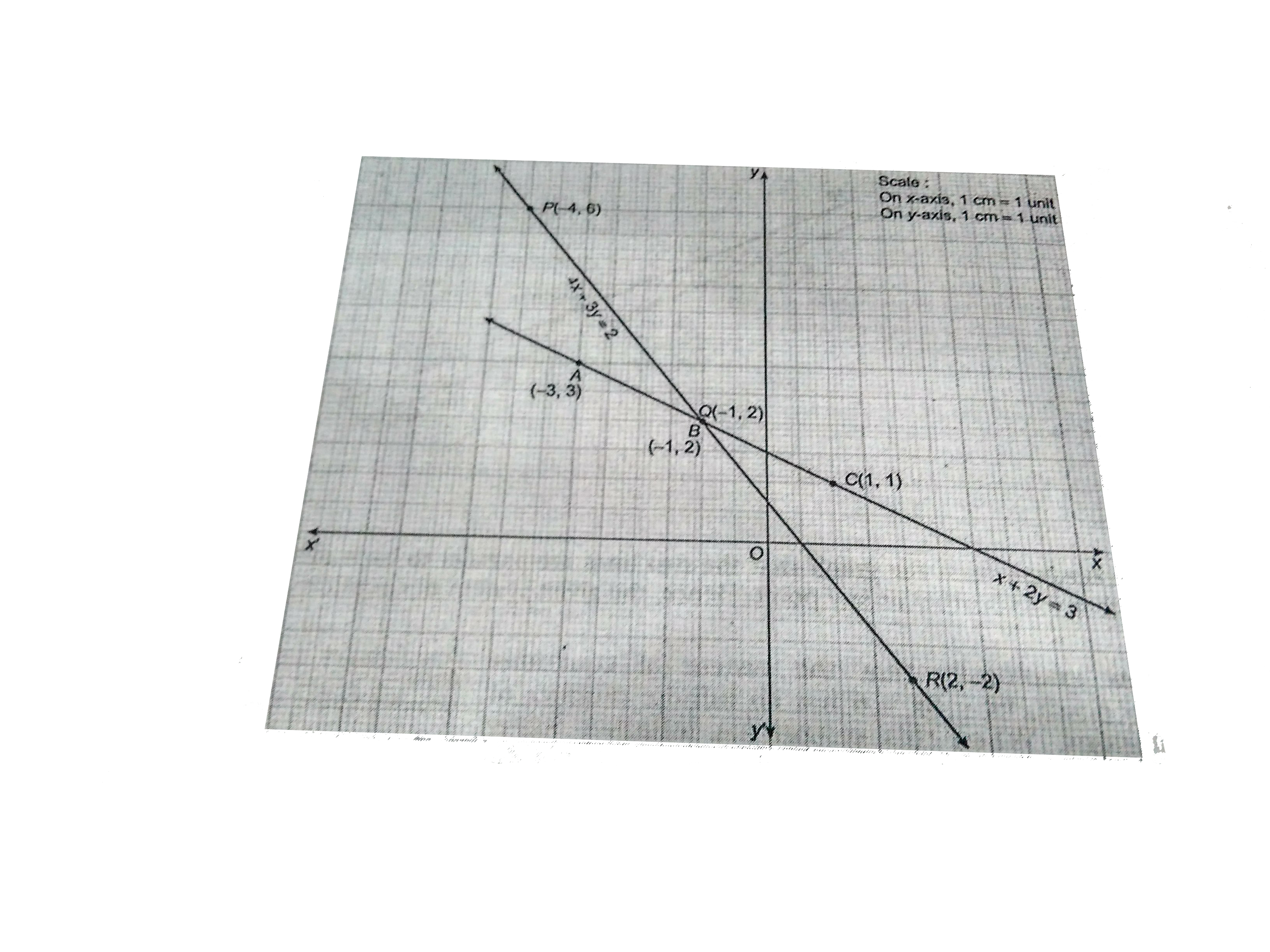
Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy



Graphing Systems Of Linear Equations




Graphing A Linear Equation 5x 2y Video Khan Academy



無料ダウンロード 3x 2y5 X5 Y




Solving Systems By Graphing And Substitution




Solving Systems By Graphing And Substitution



14 4 3d Graphing Graphing Calculator By Mathlab User Manual




Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0



Www Lcps Org Cms Lib Va Centricity Domain 2 5 notes filled out Pdf



Graph Graph Inequalities With Step By Step Math Problem Solver



Uncw Edu Ulc Services Math Documents Mat 111 Final Exam Answer Key Sp17 Pdf



Systems Of Linear Equations




Algebra Calculator Tutorial Mathpapa




Algebra Calculator Tutorial Mathpapa




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube
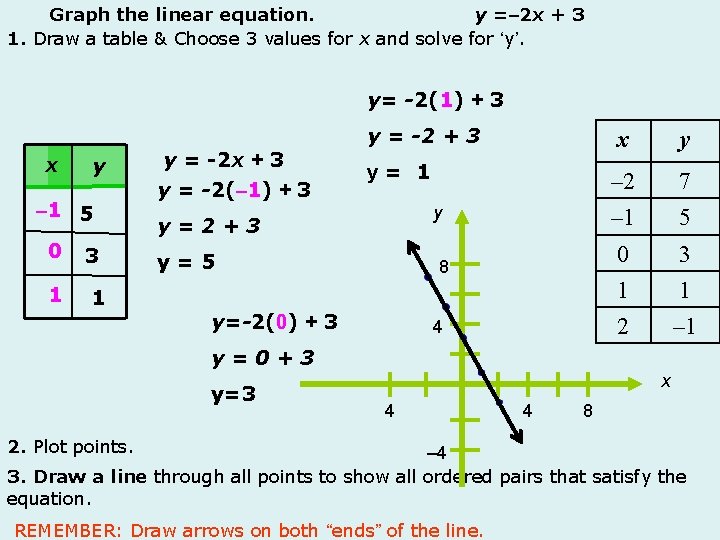



Graph The Linear Equation Yx 2 1 Draw



Graph Graph Equations With Step By Step Math Problem Solver




Is There A Solution For X For X 2 Y Sqrt 3 X 2 2 1 Mathematics Stack Exchange




Plotting All Of A Trigonometric Function X 2 Y 2 1 With Matplotlib And Python Stack Overflow
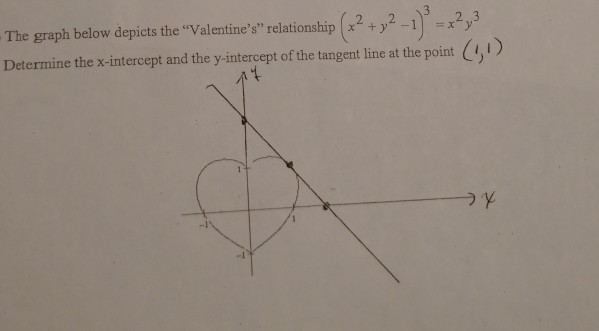



The Graph Below Depicts The Valentine S Chegg Com



Draw The Graphs Of The Following Equations 2x Y 1 X 2y 13 Find The Solution Of The Equations From The Graph Sarthaks Econnect Largest Online Education Community



Graphing Linear Inequalities
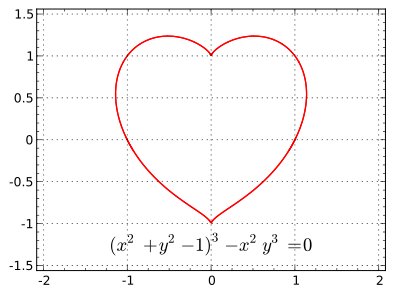



Uberfacts You Can Plot A Heart On A Graph Using The Equation X2 Y2 1 3 X2y3 0




Surfaces Part 2
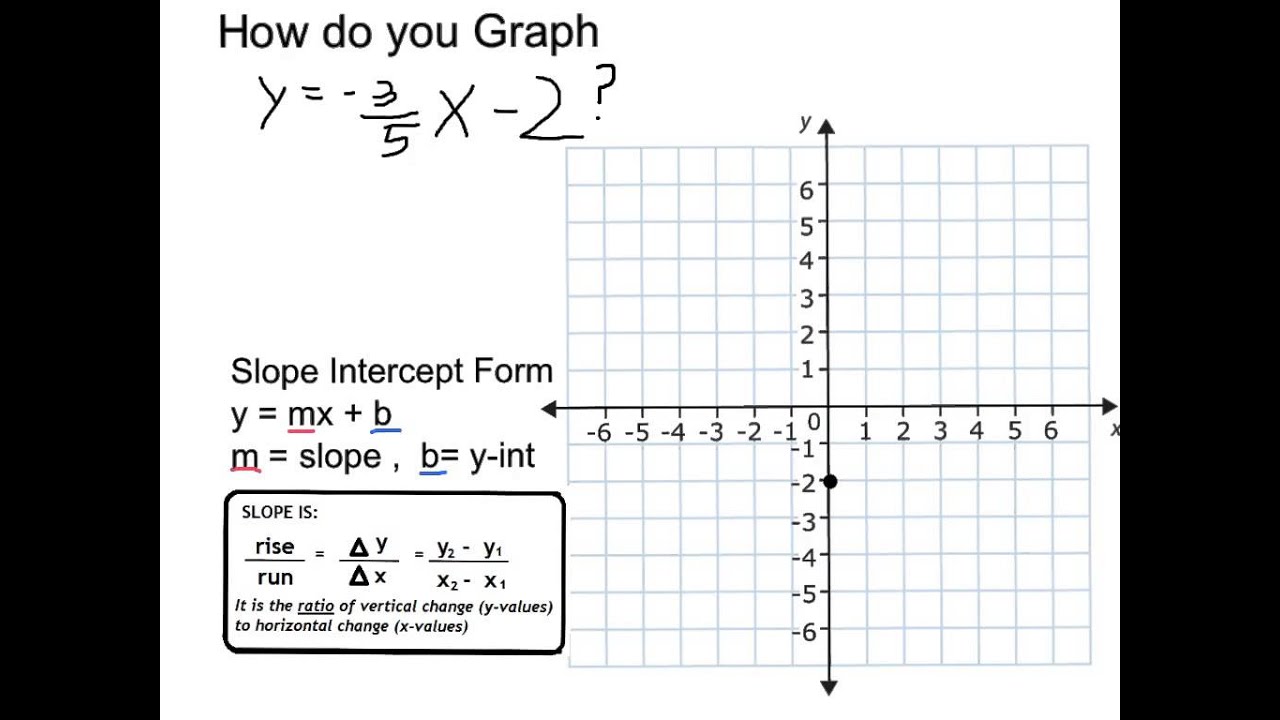



Graph Y 3 5 X 2 Youtube



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora



1




Systems Of Equations With Graphing Article Khan Academy



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora



Http Bpsbihta Com Homework 100 Class 10th Mathlesson 3 Notes Pdf




You Can Plot A Heart On A Graph I M A Nerd Heart Symbol Geek Stuff Math Pictures



Http Www Unit5 Org Cms Lib03 Il Centricity Domain 2651 Semester 1 review 15 solutions Pdf



Systems Of Linear Equations




Mrs Rivas Ppt Download




Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12




Find The Volume Of The Solid That Results When The Region Bounded By X Y 2 And X 2y 3 Is Revolved About The Y Axis Study Com
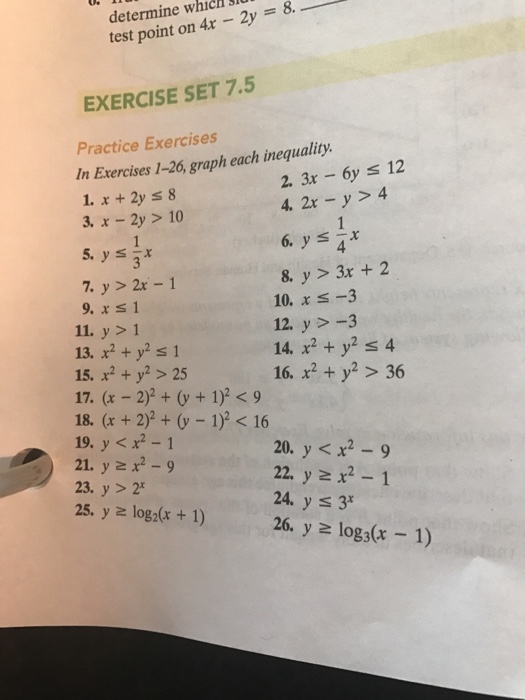



Graph Each Inequality X 2y Lessthanorequalto 8 Chegg Com




Draw The Graph Of The Equation 3x 2y 6 Find The Coordinates Of The Point Where The Graph Cuts The Y Axis




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
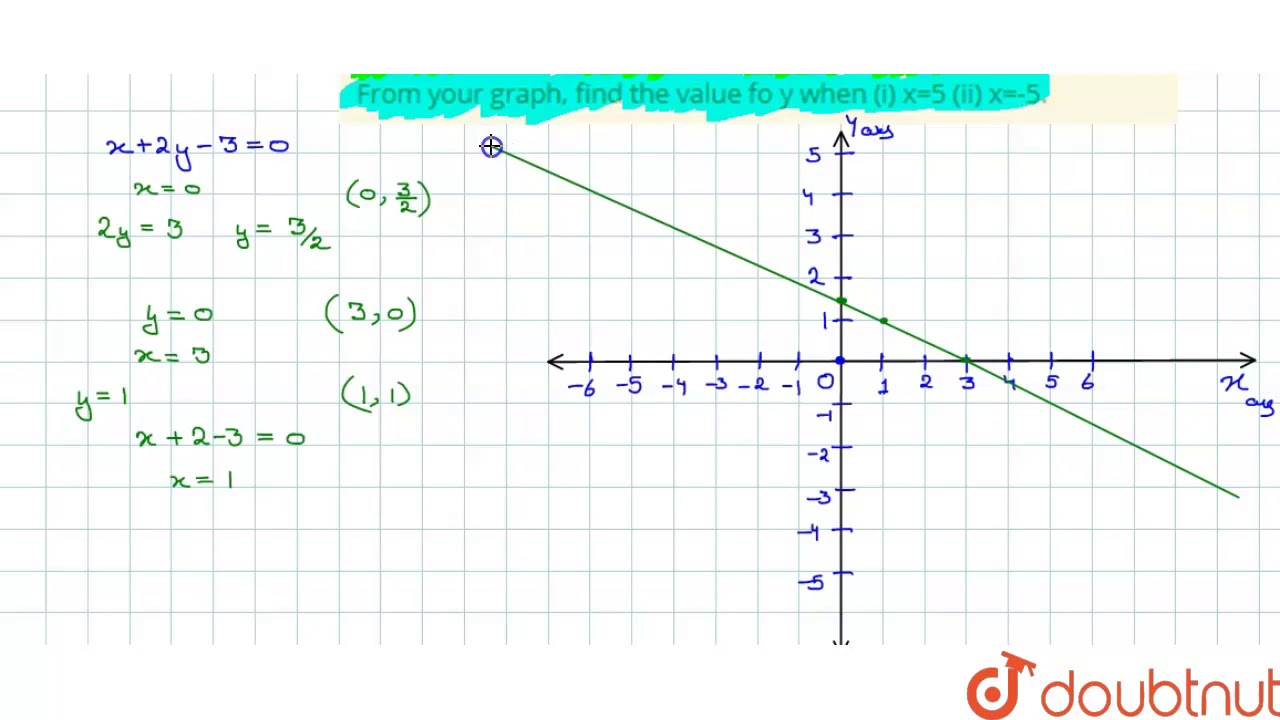



Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Fo Y When I X 5 I Youtube




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula



Quadratics Graphing Parabolas Sparknotes
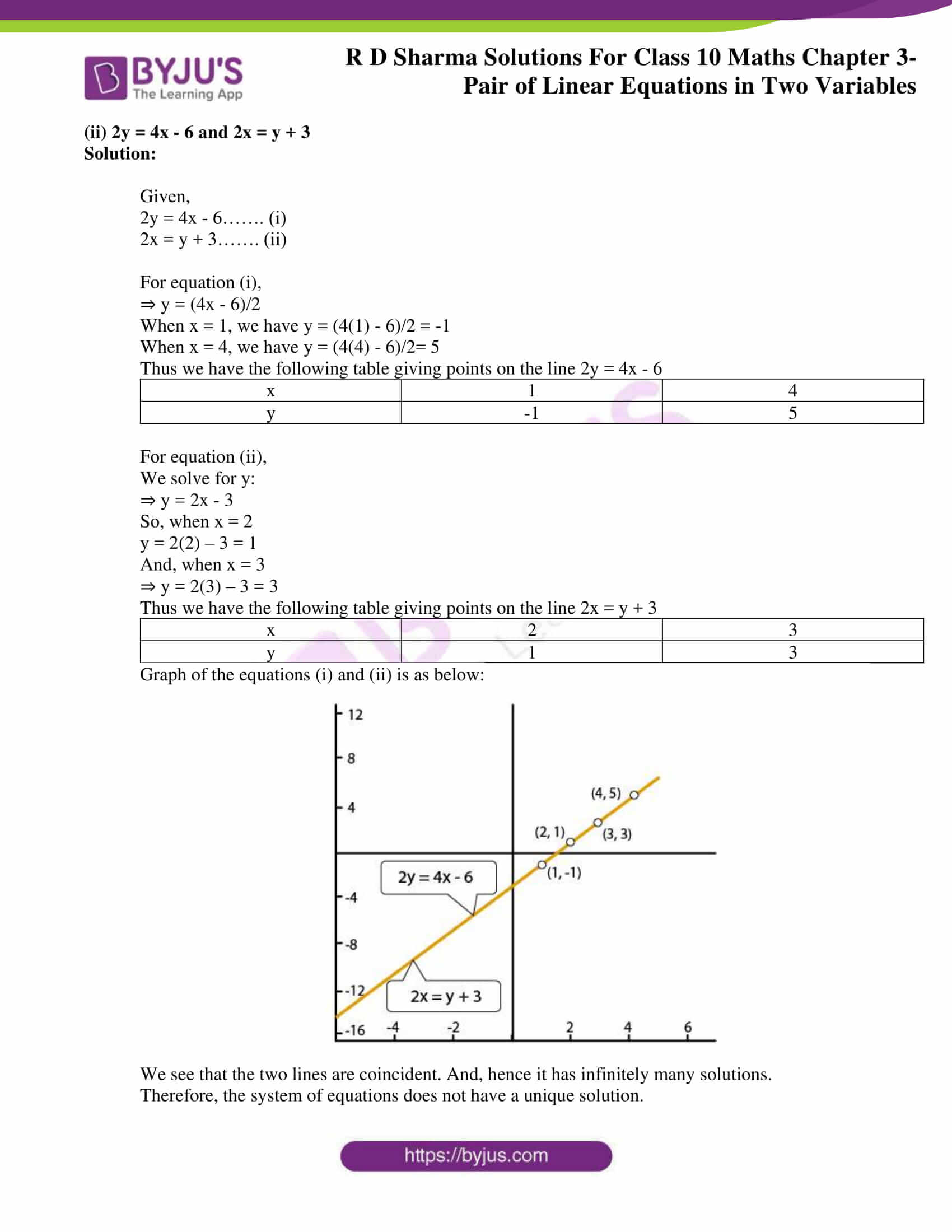



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Implicit Differentiation



Mfm2p
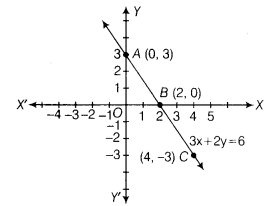



Draw The Graph Of The Straight Line Given By The Equation X 2 Y 3 1 Cbse Class 9 Maths Learn Cbse Forum



Double Integrals Over General Regions Page 2




File Heart Plot Svg Wikimedia Commons



Practice A Mathnmind




Til That A Heart Can Be Graphed Using X2 Y2 1 3 X2y3 0 Todayilearned




Math11 Learning Journal Unit 6 Leaning Journal Task Reflect On The Concepts Of Studocu



Search Q X 5e2 2by 5e2 3d0 Tbm Isch



Graph Of X 2y 3



Show That The Following System Of Linear Inequalities Has No Solution X 2y 3 3x 4y 12 X 0 Y 1 Studyrankersonline




Answered Linear Equations 26 Chapter 1 Problems Bartleby




Identify The Type Of Graph That Each Equation Has Chegg Com




2 2 Y 3 Cheap Online




Draw The Graph Of The Equation 3x 2y 4 And X Y 3 0 On The Same Graph Paper Find The Coordinates Of The Point Where The Two Graph Lines Intersect



To Solve Simultaneous Equations X 2y 4 3x 6y 12 Graphically Following Are The Ordered Pairs Sarthaks Econnect Largest Online Education Community



Solution How To Graph X 2y 3




Solutions To Implicit Differentiation Problems




Systems Of Linear Equations Free Math Help
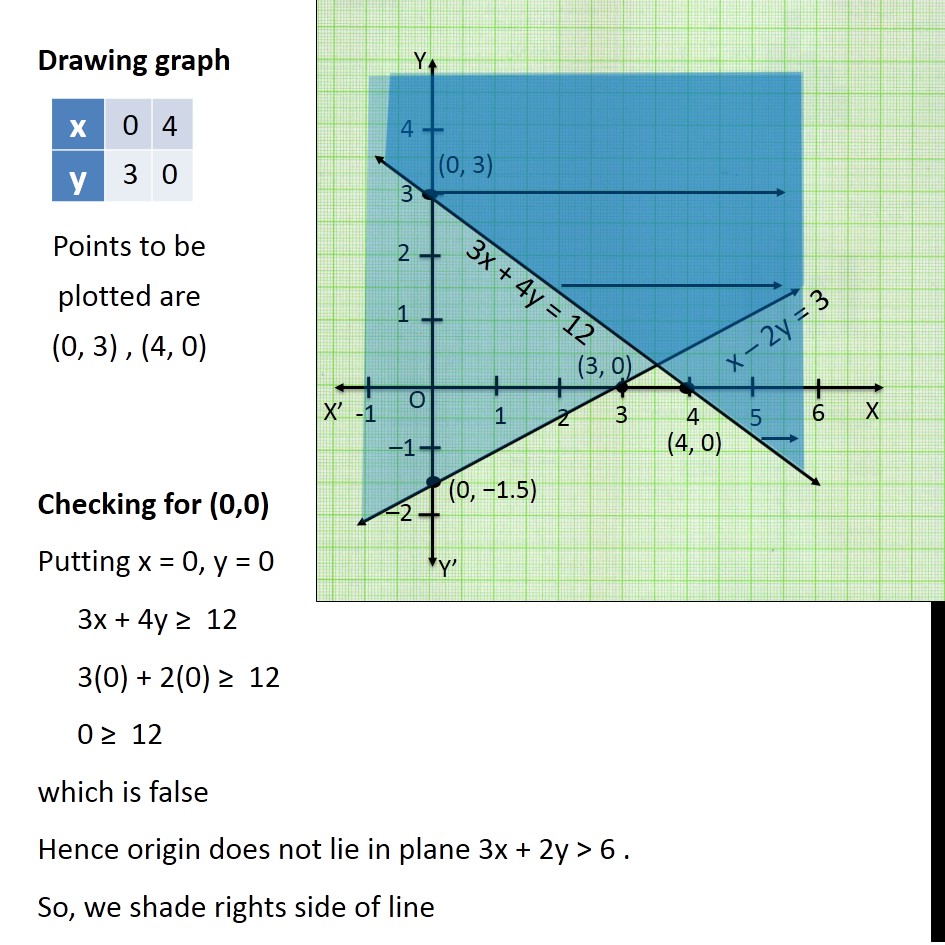



Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12



1
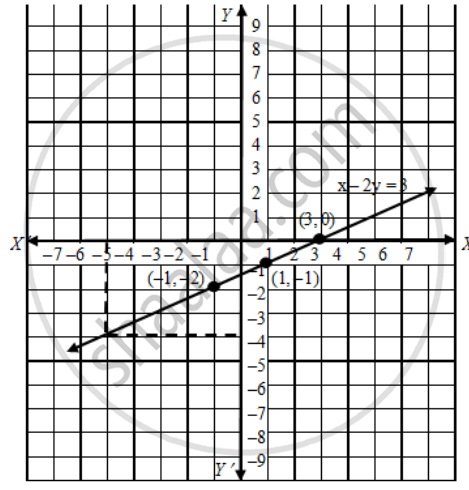



Draw A Graph Of The Line X 2y 3 From The Graph Find The Coordinates Of The Point When I X 5 Ii Y 0 Mathematics Shaalaa Com



Simultaneous Equations Gmat Math Study Guide



ʇɥƃiluooɯ ǝiʇɐs 𖥶 X 2 Y 2 1 3 X 2y 3 0 Http T Co Ovno91ma5r




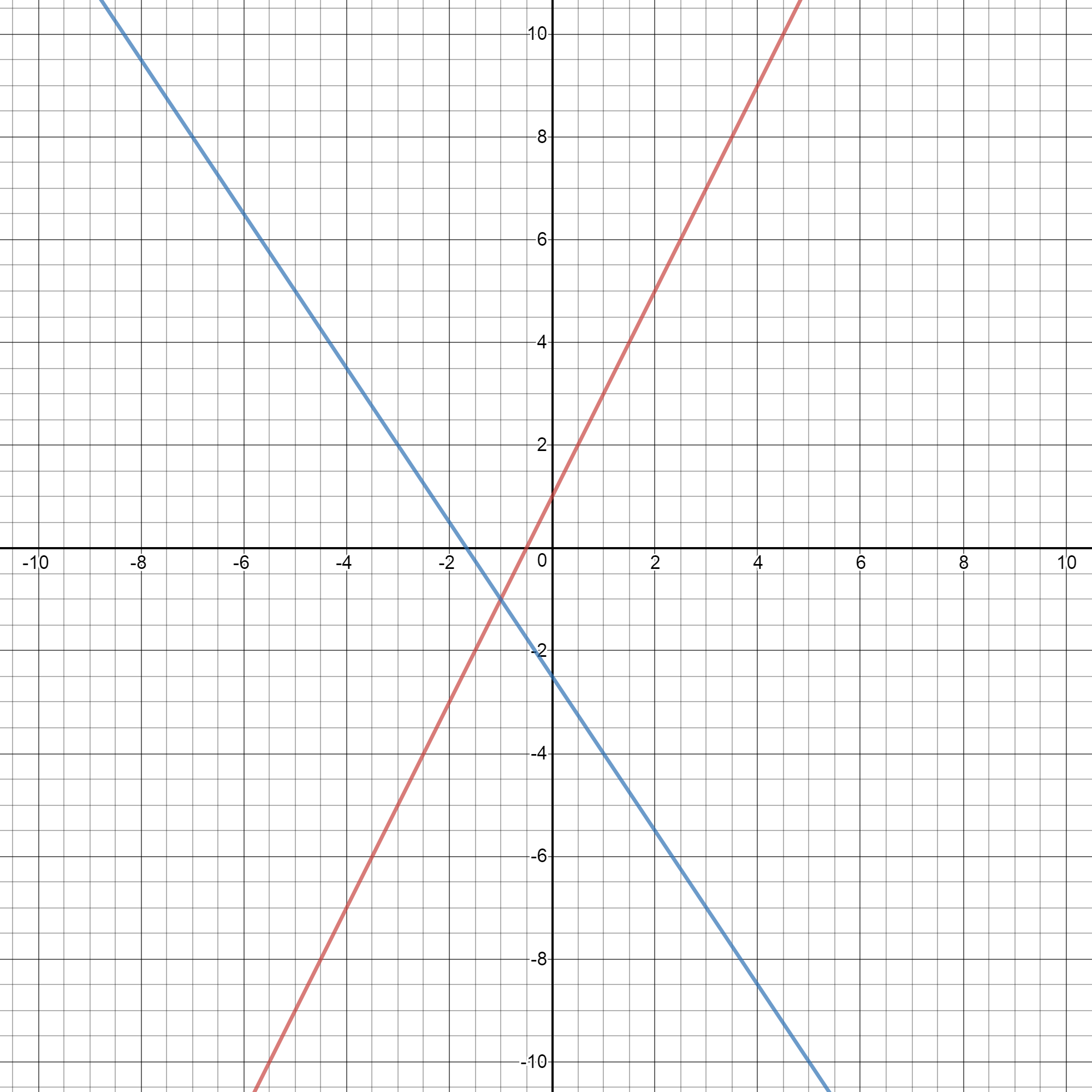
Solve The Following System Of Linear Equations Graphically 3x 2y 1 0 2x 3y 6 0 Shade The Region Brainly In




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper
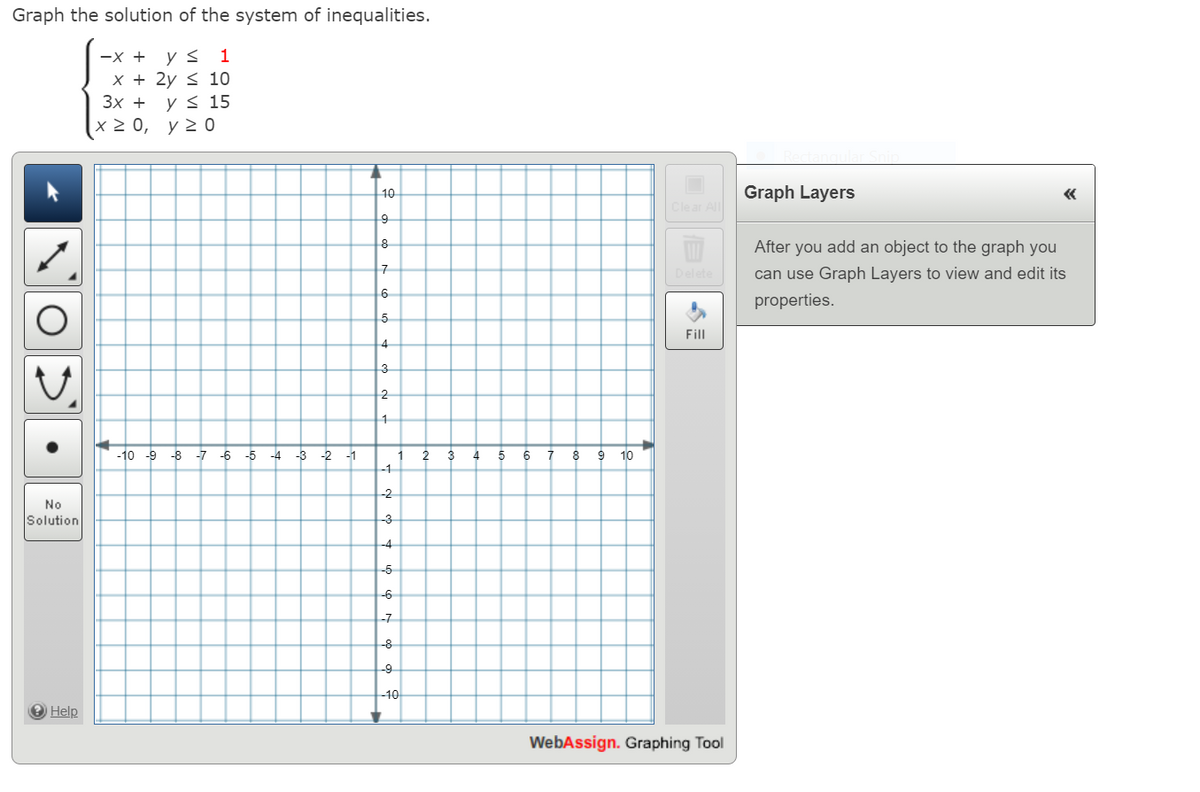



Answered Graph The Solution Of The System Of Bartleby



Http Mansfieldalgebra1 Weebly Com Uploads 1 0 4 4 Rc 2 Answer Key Pdf



Plotting A Linear Equation


